2022-01-21 11:14:32 大理华图考试网 http://dali.huatu.com/ 文章来源:云南分院
在公考行测数量关系中,行程问题属于一个比较难的知识点,相遇追及问题又是难点中的难点,灵活多变,很多考生把握不住,感觉比较头疼。但是有些小题型是有固定解题步骤可循的,接下来图兔就带大家来学习一个相遇追及问题中比较特殊的题型——直线型多次相遇问题。

扫码进入省考交流群
首先,我们要先知道什么是直线型多次相遇,比如两个人从甲地和乙地同时出发,相向而行,直到相遇,这属于我们比较常见的相遇问题,也可以称作第一次相遇。当这两个人相遇完之后继续往前走,会分别到达对方的出发点,此时立即折返,两人会再次在甲乙两地之间相遇,也可以称作第二次相遇,当这两个人相遇完之后再继续往前走……也就是我们所说的直线型多次相遇中的两端出发型。还有一个是同端出发型,即两人都从甲地出发,同时前往乙地,若两人速度不同,则其中一人会先到达乙地,立即原路折返,和迎面而来的另一人相遇,后面的相遇类似于两端出发型。
然后,我们来学一下这个问题的题型特征和解题方法,题型特征其实就是题干中出现“第二次相遇,再次相遇,第三次相遇……”。两人相遇次数与共走的路程是有联系的(设甲乙两地相距S),①两端出发型,第n次相遇,两人共走(2n-1)S,根据相遇问题核心公式:总路程S=速度和×相遇时间t,得t=;②同端出发型,第n次相遇,两人共走2nS,t=。当题干中条件充分时,我们可以用公式法直接解题。
下面我们来练习一道题。
【例1】某高校两校区相距2760米,甲,乙两同学从各自校区同时出发到对方校区,甲的速度为70米/分钟,乙的速度为110米/分钟,在路上二人第一次相遇后继续行进,到达对方校区后马上回返,那么两人从出发到第二次相遇需要多少分钟?
A.32
B.46
C.61
D.64
【答案】B
【解析】观察此题,问题中出现“第二次相遇”,属于直线型多次相遇,由“甲,乙两同学从各自校区同时出发到对方校区”,两端出发型,根据我们的解题方法,t=,代入数据,得t==46(分钟)。因此,选择B选项。
上面这个题属于直接套用公式即可得出答案,当然还有相对比较复杂的题,我们再来看一道。
【例2】甲车从A地、乙车从B地同时出发匀速相向行驶,第一次相遇距A地100千米,两车继续前进到达对方起点后立即以原速度返回,在距离A地80千米的位置第二次相遇,则AB两地相距多少千米?
A.170
B.180
C.190
D.200
【答案】C
【解析】观察此题,题干中出现“第二次相遇”,属于直线型多次相遇,由“甲车从A地、乙车从B地同时出发匀速相向行驶”,两端出发型,但是缺少两车的速度以及第二次相遇所需时间,无法一步公式算出AB两地相距距离。那怎么办呢?别着急,我们针对这种题有对应的解决办法——比例法()。我们分析题干,设AB两地相距S千米,第一次相遇距A地100千米,则甲走了100千米,两人共走S;第二次相遇距A地80千米,则说明甲还需再走80千米才算走一个往返,即此时走了(2S-80)千米,两人共走(2n-1)S=3S千米。代入比例,得,解得S=190(千米)。因此,选择C选项。
有些同学会说,这个方法万一忘了咋办呀?最后我们再讲一个应对一些特殊题目的猜题技巧,以供大家不时之需,看一道题。
【例3】甲、乙两车分别从A、B两地同时出发相向而行,速度之比为3∶4,在途中第一次相遇后,两车仍以原速前行,当各自到达终点后立即返回,又在途中第二次相遇,这时甲车距A地50千米,则A、B两地间距()千米。
A.70
B.87.5
C.95
D.116.7
【答案】A
【解析】观察此题,题干中出现“第二次相遇”,属于直线型多次相遇,由“甲、乙两车分别从A、B两地同时出发相向而行”,两端出发型。也是缺少一些条件,需要用比例法来解,如果忘了比例法怎么办呢?我们来猜一下,已知两车速度之比为3∶4,也就意味着两人速度和是7的倍数,根据路程=速度×时间,猜测路程也是7的倍数,观察选项,只有A选项是7的倍数,因此猜A选项。
当然了,这个只是一个猜题技巧,不能确保肯定对。
总结一下,当题干条件充分时,可以使用公式法,直接算出时间或者是总路程;当题干条件不足,只有某几次相遇时的一些距离,需要使用比例法求解;当没时间或者忘掉如何算时,可以根据倍数特性猜题。
以上就是数量关系直线型多次相遇问题的题型和对应的方法,希望大家熟练掌握,今后遇到此题型可以快速得出正解。
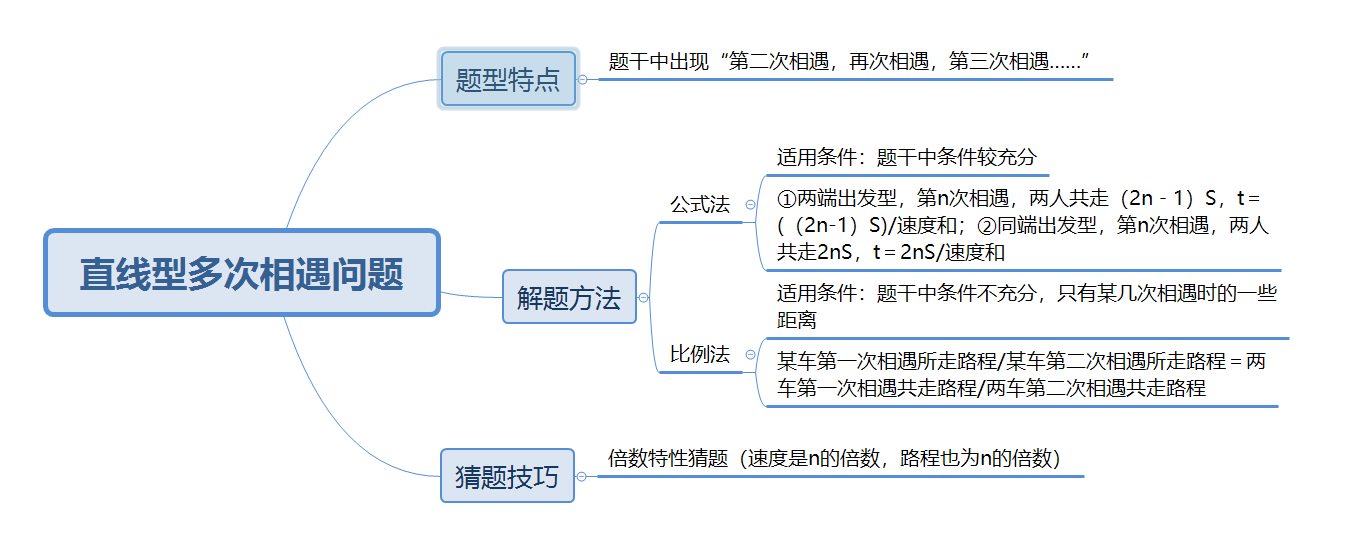
思维导图

更多考试资讯请关注我们