您当前位置：大理人事人才网 > 大理公务员 > 试题资料 > 2022公务员行测数量关系中最值问题的解题小技巧

2022公务员行测数量关系中最值问题的解题小技巧

2022-01-29 17:57:03 大理华图考试网 http://dali.huatu.com/ 文章来源：云南分院

【导读】大理华图从事公务员、事业单位、教师、医疗等培训辅导，同时整理多类招考信息，为您做就业小帮手，更多考试资讯请关注大理华图公众号，大理华图官网https://dali.huatu.com/

在公务员考试行测科目中有这样的一类题目：让我们求某一个量的最大/最小值能够取到多少，我们把它称之为最值问题。最值问题是数量关系模块中的一个高频考查题型，难度适中，考查形式比较固定。只要我们学会了关于这类题目的解题思路，就可以帮助我们在考试中解决这类题目，轻松拿分。因此，接下来我们就一起来学习最值问题的解题小技巧。

一、了解最值问题

首先从考查题型来看，常考的题型主要有以下三大类：最不利构造、数列构造、多集合反向构造。具体每一类题型的题型特征和解题思路如下思维导图：

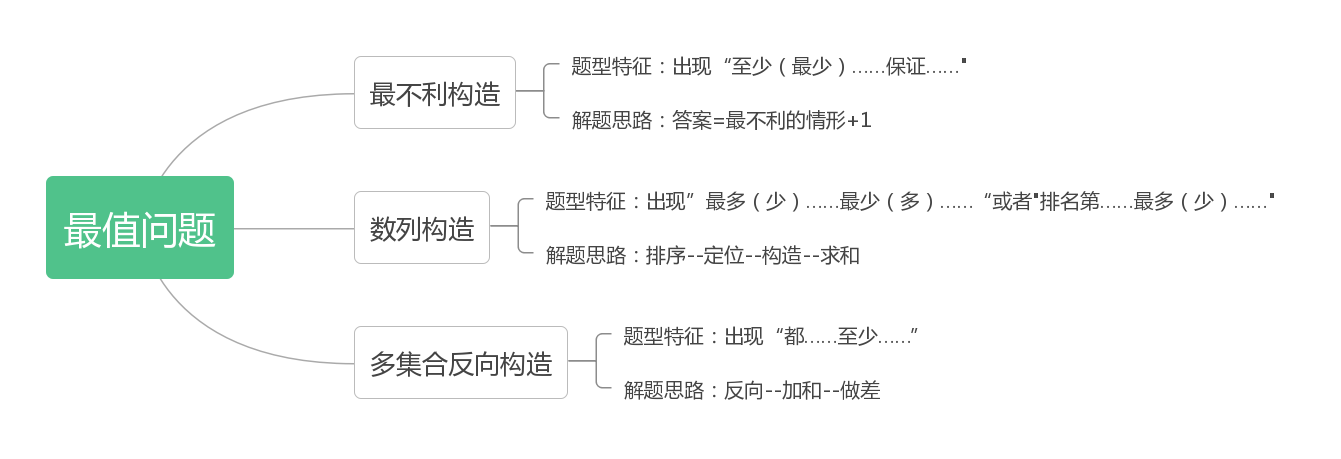
其次从考查题量来看，最值问题在最近几年的国考或者联考中都经常出现。以国考为例，最近5年国考中关于最值问题的考查题量如下表：

	2021年	2020年	2019年	2018年	2017年
最不利构造		1		1
数列构造	1			1	1
多集合反向构造			1

真题实战

【例1】(2019重庆)某地区招聘卫生人才，共接到600份不同求职者的简历。其中，临床、口腔、公共卫生和护理专业分别有200人、160人、140人和100人，问至少有多少人被录用，才能保证一定有140名被录用者专业相同?

A.141B.240

C.379D.518

【解析】第一步，根据题目提问中出现特征“至少…才能保证…”，确定本题考查最不利构造问题。

第二步，因为要保证一定有140名录用者专业相同，所以最不利的情况数=140-1=139(名)，题目中有临床、口腔、公共卫生和护理四种不同专业，则所有的最不利情况数=139+139+139+100=517(名)，则答案=所有的最不利情况数+1=517+1=518(名)。即至少有518人录用，才能保证一定有140名录用者专业相同。

因此，选择D选项。

【例2】(2021广东)某街道服务中心的80名职工通过相互投票选出6名年度优秀职工，每人都只投一票，最终A、B、C、D、E、F这6人当选。已知A票数最多，共获得20张选票;B、C两人的票数相同，并列第2;D、E两人票数也相同，并列第3;F获得10张选票，排在第4。那么B、C获得的选票最多为()张。

A.11B.12

C.13D.14

【解析】第一步，本题考查最值问题，属于数列构造类。

第二步，80人共投出80张票，若使得B、C获得的选票最多，则A、D、E、F票数尽量少。已知A票数最多，共获得20张选票，F获得10张选票;因此尽量让D、E的票数最少，且高于F，均是11张选票。

第三步，B、C共获得最多票数为80-20-10-11×2=28(张)，B、C两人的票数相同，则B=C=28÷2=14(张)。

因此，选择D选项。

【例3】(2018-广东县级-27)某软件公司对旗下甲、乙、丙、丁四款手机软件进行使用情况调查，在接受调查的1000人中，有68%的人使用过甲软件，有87%的人使用过乙软件，有75%的人使用过丙软件，有82%的人使用过丁软件。那么，在这1000人中，使用过全部四款手机软件的至少有()人。

A.120B.250

C.380D.430

【解析】第一步，本题考查多集合反向构造。多集合反向构造解题方法是：反向——求和——做差。