2022-02-15 13:37:27 大理华图考试网 http://dali.huatu.com/ 文章来源：云南分院
在行测数量关系的学习过程中，许多小伙伴对于多集合反向构造这一类题型的掌握仍然有所欠缺，其实此类题型的解法相对固定，小伙伴只要经过一定的练习就能熟练掌握。所以今天我们一起学习下吧。
在学习多集合反向构造最开始，首先要对此类题型有初步的了解。此类题型归属于集合问题，即容斥问题;然而它又融合了极值的思想，需要同学们用最值思维去解题。通常而言，此类题型会出现关键词“都……至少……”，即要求同时满足多种条件的情况数，想办法求该情况数的极值。文字比较抽象，我们画出图来帮助大家更好地理解。
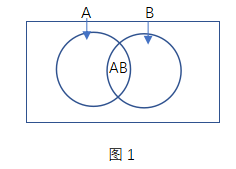
多集合反向构造类的题目就像上图(图1)所示，通常会让我们求的是同时满足多个条件的区域的极值，比如此题就是问AB的最小值为多少。在图形中，AB代表的区域是两个集合相交的部分，从图中可以看出，两个集合“离得越开，AB区域越小”，转化为数学语言即求的是两个集合交集的最小值。如果题目没有限制，两个集合互相独立的时候，该交集的最小值就为0了。但是一般情况下，题目中两个集合都会有交集，所以这个时候我们就不太容易从正面对AB的极值进行量化，因此我们需要转变思维，从反方向去探讨AB的极值。
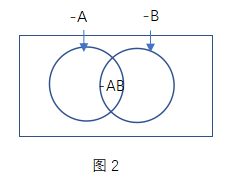
如上图(图2)所示，我们再看这个集合，分别代表着不满足A的情况数以及不满足B的情况数，正中间的交集为同时不满足A和B的情况数，那么两个集合组合起来的图形代表着什么呢?它应该代表着“不满足A或者不满足B的情况数”。而空白的部分，是“不满足A或不满足B的情况数”的反面，即“同时满足A和B的情况数”——AB的情况数。此时想求AB的最小值就简单许多了：只要使“不满足A或者B的情况数”尽量地大，这时候AB地值就相对变小。在-A和-B这两个集合无交集的时候，AB有最小值，如下图(图3)所示。
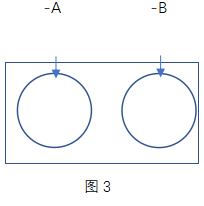
此时我们想求AB的最小值，只需用总的情况数减去反向构造出的集合之和就行了，即
。通过此题，可以归纳出多集合反向构造的解题步骤：反向——求和——做差。之后我们在遇到此类题型，我们只需要按照这三步，就可以解题。
好了，相信小伙伴们已经摩拳擦掌了，我们赶紧用例题来检验一下学习的内容吧。
【例】某机构对全运会收视情况进行调查，在1000名受访者中，观看过乒乓球比赛的占87%，观看过跳水比赛的占75%，观看过田径比赛的占69%。这1000名受访者中，乒乓球、跳水和田径比赛都观看过的至少有：：
A. 310人
B. 440人
C. 620人
D. 690人
【答案】A
【解析】第一步，本题考查最值问题，属于多集合反向构造。
第二步，根据多集合反向构造的思路，“反向——求和——做差”。
反向：未观看乒乓球比赛的人数为1000×(1-87%)=130人，未观看跳水比赛的人数为1000×(1-75%)=250人，未观看田径比赛的人数为1000×(1-69%)=310人。
求和：三种比赛有人没看过的最多有130+250+310=690人。
做差：三种比赛都观看过的至少为1000-690=310人。
因此，选择A选项。
今天的学习就先到这里，小伙伴下来还需要多做几个例题巩固一下哦。
更多考试资讯请关注我们
京公网安备11010802021470号