2022-01-22 11:15:50 大理华图考试网 http://dali.huatu.com/ 文章来源:云南分院
什么是方程法呢?大家回顾一下,我们在初中就学过,有未知数的等式就叫做方程,相比较其它方法来讲,方程法的应用,更具有普遍性,我们公考数量关系中的大部分题目都可以用方程法来求解,所以说方程法也是一个很重要的方法。而且大家对它也应该比较熟悉,相信大家在接下来的学习中能够掌握。

扫码进入省考交流群
那么方程的学习我们主要掌握什么呢?其实可以分为两部分:第一部分是方程和方程组,第二部分是不定方程和不定方程组。
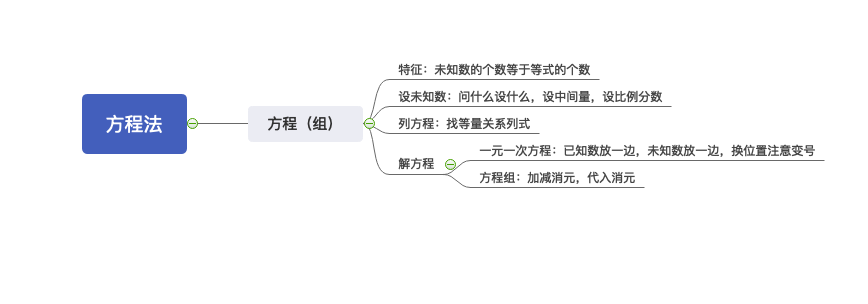
那我们先来学习第一种:方程和方程组。这里的方程主要指的是一元一次方程,只含有一个未知数,方程组说的就是二元一次方程组,是指含有两个未知数。好的,刚才老师带着大家回顾了一下方程和方程组的概念,那么我们如何去运用它呢?接下来我们看一下用方程解题的三个步骤:
第一步,设未知数。这是最重要的一个环节,我们有几种设未知数的方式。
第一种叫设直接未知数。换句话说就是“问什么设什么”,如果方便计算,优先选择设直接未知数,问人数设人数,问钱数设钱数。
第二种叫做设中间量。有的时候我们设直接未知数不便于列数或者求解,可以引入一个中间量。老师给大家简单举个例子:甲的年龄比丙年龄的2倍还多13,甲比乙大一岁,问甲的年龄为多少?那这道题我们直接设甲肯定不太好列式,我们可以设丙为X,甲:2x+13乙:2x+12。我问甲的年龄,那我设丙为x,那丙就是中间量。这个中间量其实就是一个桥梁。
第三种就是设比例未知数。什么是比例未知数?比如说题目中出现“甲:乙=3:5”让分别求甲和乙,那大家可能会想,这个可不可以用倍数特性来解决呢?当然可以,但是如果说选项都是3的倍数,这个问题是不就无法解决了?那这种情况怎么办?我们是不是可以用方程来解决呢?我可以设甲为3x,乙为5x,也就是是三份和五份。再比如说这样的情况:甲=总数*1/3,乙=总数*1/5,都与总数有关,但这个时候我们如果直接设总数为x,后面就会出现分数,是不不太好解?那怎么假设更好呢?我们是不可以直接设总数为15x,那甲就是5x,乙就是3x。我们把这样的设法就叫做设比例未知数,其实也是设份数。
第二步,列方程。我们要想求未知数就需要把未知数放在等量关系当中去,这就是列方程,有时候这个等量关系不是很明显,就需要我们多研读提干,深度挖掘。
第三步,解方程。我们行测考试都是选择题,所以我们必须要求解出答案,才能选出来,那我们怎么去解方程呢?一元一次方程,直接移项,已知数放一边未知数放一边,注意换位置的时候要变好,二元一次方程,消元法,这里大家要注意,尽量不要消所求量,也就是题干中让你求x,你就不要把x消了。如果计算比较复杂,轻易解不出来的时候,可以借助带入排除法,就是可以将选项直接代入到方程中去,找到满足条件的答案即可。
那方程的基本概念和步骤我们已经介绍完了,接下来我们一起来看一下例题。
【例】(2017联考)小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送达1枚完整无损的鸡蛋,可得运费0.1元;若有鸡蛋破损,不仅得不到该枚鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那么,在运送过程中,鸡蛋破损了:
A.20枚
B.30枚
C.40枚
D.50枚
小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送达1枚完整无损的鸡蛋,可得运费0.1元;若有鸡蛋破损,不仅得不到该枚鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那么,在运送过程中,鸡蛋破损了?本题目等量关系比较明显,问的是鸡蛋破损了多少?那么我们问什么设什么,所以设鸡蛋破损X枚,鸡蛋破损X枚那么完好的鸡蛋数为25000-X。设好未知数,我们来看一下题干中存在怎样的等量关系:运送1枚完好无损的鸡蛋可得0.1元,破损则需要赔偿0.4元,且总共得到的运费是2480元。那我们这边就可以列出等量关系运送完好的运费减去赔偿的钱数是最后运送得到的总费用,我们把破损了X枚鸡蛋代入等量关系中,可以得到方程:0.1(25000-X)-0.4X=2480解方程得到X=40,那么我们选项选C。
最后我们来总结一下吧,请看下图:

更多考试资讯请关注我们